3.5. Расчёт номинального тока

Для того, чтобы шаговый двигатель выдавал максимальный вращающий момент, но при этом не перегревался, важно правильно задать такую техническую характеристику, как номинальный ток.

Чем больше ток в обмотке двигателя, тем больше вращающий момент на оси. Важно помнить, что с увеличением протекающего через обмотки тока, выделяемая тепловая мощность двигателя увеличивается. Чтобы двигатель мог работать длительное время, выделяемая тепловая мощность (Закон Джоуля — Ленца) должна быть меньше мощности рассеяния. Мощность рассеяния можно рассчитать исходя из документации на двигатель.

3.5.1. Расчеты на базе параметров униполярного полношагового режима

Мощность рассеяния равна

\[P = n \cdot R_u I_u^2,\]

где \(R_u\) - сопротивление обмотки в униполярном режиме, \(I_u\) - ток через одну обмотку в униполярном режиме, \(n\) - колличество одновременно работающих обмоток.

Рассмотрим для примера ST2818M1006. Таблица в документации показывает, что в полношаговом режиме одновременно работает две обмотки (n = 2) в униполярном режиме, т.е. \(P = 2 R_u I_u^2\). Контроллеры моторов поддерживают только биполярный режим управления. Чтобы перейти от униполярного в биполярный режим, соединим обмотки каждой фазы последовательно, сопротивление возрастёт, \(R_b = 2 R_u\), где \(R_b\) - сопротивление последовательно соединенных обмоток для биполярного режима управления.

Алгоритм управления в контроллерах моторов работает в микрошаговом режиме и поддерживает ток так, что в одной обмотке ток меняется по функции \(I_a \sin(\phi)\), в другой обмотке ток меняется по функции \(I_a \cos(\phi)\), где \(I_a\) - амплитуда тока. Тепловая мощность, выделяемая двумя обмотками в любой момент времени

\[P = R_b I_a^2 \sin^2(\phi) + R_b I_a^2 \cos^2(\phi) = R_b I_a^2\]

Получим уравнение, приравняв мощности, из которого найдём, что \(I_a = I_u\).

3.5.2. Расчеты на базе параметров биполярного полношагового режима

Мощность рассеяния равна \(P = n \cdot R_b I_b^2\), где \(R_b\) - сопротивление обмотки в биполярном режиме, \(I_b\) - ток через одну обмотку в биполярном режиме, n - колличество одновременно работающих обмоток.

Рассмотрим для примера ST2018S0604. Таблица в документации показывает, что в полношаговом режиме одновременно работает две обмотки (n = 2) в биполярном режиме, т.е. \(P = 2 R_b I_b^2\).

Тепловая мощность, выделяемая на обмотках двигателя, управляемого контроллерами моторов, по-прежнему

\[P = R_b I_a^2 \sin^2(\phi) + R_b I_a^2 \cos^2(\phi) = R_b I_a^2\]

Получим уравнение, приравняв мощности \(2 R_b I_b^2 = R_b I_a^2\). Найдем, что \(I_a = \sqrt{2} \cdot I_b\).

3.5.3. Связь со среднеквадратичным током

Переменный ток в каждой обмотке двигателя может характеризоваться своим среднеквадратичным значением за период

\[I_{rms} = \sqrt{\frac{1}{2 \pi} \int\limits_0^{2 \pi} (I_a \sin(\phi))^2 \, \mathrm{d}\phi} = \frac{I_a}{\sqrt{2}}\]

Тепловое выделение одной обмотки связано со среднеквадратичным током через неё \(P_1 = R_b I_{rms}^2\). Обе обмотки идентичны \(P_1 = P_2\). Общая тепловая мощность двигателя под управлением контроллера моторов \(P = P_1 + P_2 = 2 R_b I_{rms}^2\).

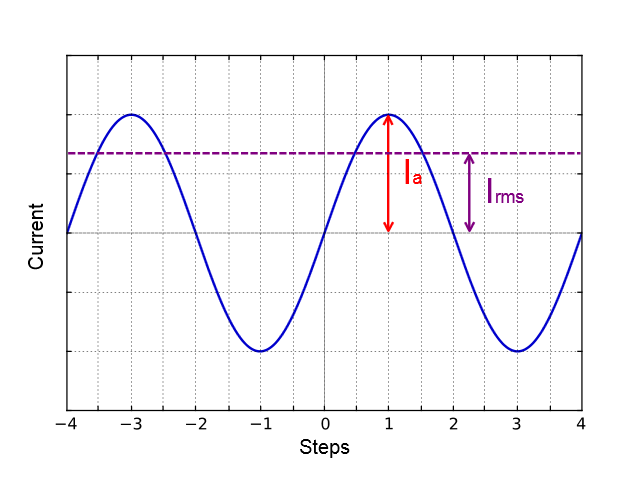
Из вышеописанного следует, что \(I_{rms} = \frac{I_u}{\sqrt{2}}\), а также \(I_{rms} = I_b\).

3.5.4. Настройка номинального тока

Контроллеры моторов способны принимать значение номинального тока в виде амплитуды тока Ia или в виде среднеквадратичного значения Irms. Выбор того, каким способом интерпретировать входное значение номинального тока, определяется отсутствием/наличием соответственно флага`ENGINE_CURRENT_AS_RMS` в поле EngineFlags структуры engine settings . При настройке номинального тока в XILab следует правильно указывать способ интерпретации тока. Контроллеры моторов в этом случае будут обеспечивать максимальный допустимый момент, не перегревая двигатель.

Для всех моторизованных позиционеров Standa подготовленные конфигурационные файлы содержат номинальный ток, заданный среднеквадратичным значением. Соответсвующий флаг установлен. Таким образом, двигатели работают на оптимальных параметрах.